Information-theoretic generalization bounds for learning and metalearning

Our funding application “evaluated mutual information bounds for learning and metalearning”, which was submitted to the Wallenberg AI Autonomous Systems and Software program (WASP) call for academic PhD student projects, has been approved.

This project will be performed in collaboration with Prof. Rebecka Jörnsten, Division of Applied Mathematics and Statistics, Department of Mathematical Sciences, Chalmers.

Within this project, we have just announced a PhD student vacancy.

The selection vector $S^n$ identifies $n$ entries of the sample matrix $Z^{2n}$ (the entries marked in red) that are then used for training and result in the DNN weights $W$, drawn from the posterior distribution $P_{W | Z^n(S^n)}$. Some of the tightest bounds available for this setup depend on the mutual information $I(W;S_i | Z^{2n})$, $i=1,\dots, n$. The bounds to be obtained within this research program will depend instead on the mutual information $I(\ell(W,Z_i), \ell(W,Z_{n+i}); S_i | Z^{2n})$, $i=1,\dots, n$. Here, $\ell(W,Z_i)$ and $\ell(W,Z_{n+i})$ denote the loss function computed for a DNN with weights $W$ when given as input the data samples $Z_i$, and $Z_{n+i}$, respectively.

Project description

Deep neural networks (DNNs) are a crucial component of the data-scientist toolbox. Indeed, over the last decade, the number of research fields in which deep learning algorithms have become part of state-of-the-art solutions has increased significantly, encompassing areas as diverse as computer vision, speech recognition, and natural language processing.

The empirical success of DNNs is, however, a puzzle to theoreticians. Despite many recent efforts, a theory that explains satisfactorily why DNNs perform so well and that guides their design is still missing. As the use of DNNs moves from academic-driven research, conducted on simple prototypes, to large-scale safety-critical industrial applications such as autonomous driving, this state of affairs is becoming increasingly unsatisfactory. DNNs can no longer be used as black boxes, and their design cannot be simply based on empirical studies. There is an urgent need to develop theoretical tools that provide guarantees on the performance of DNNs and inform their design.

The challenge

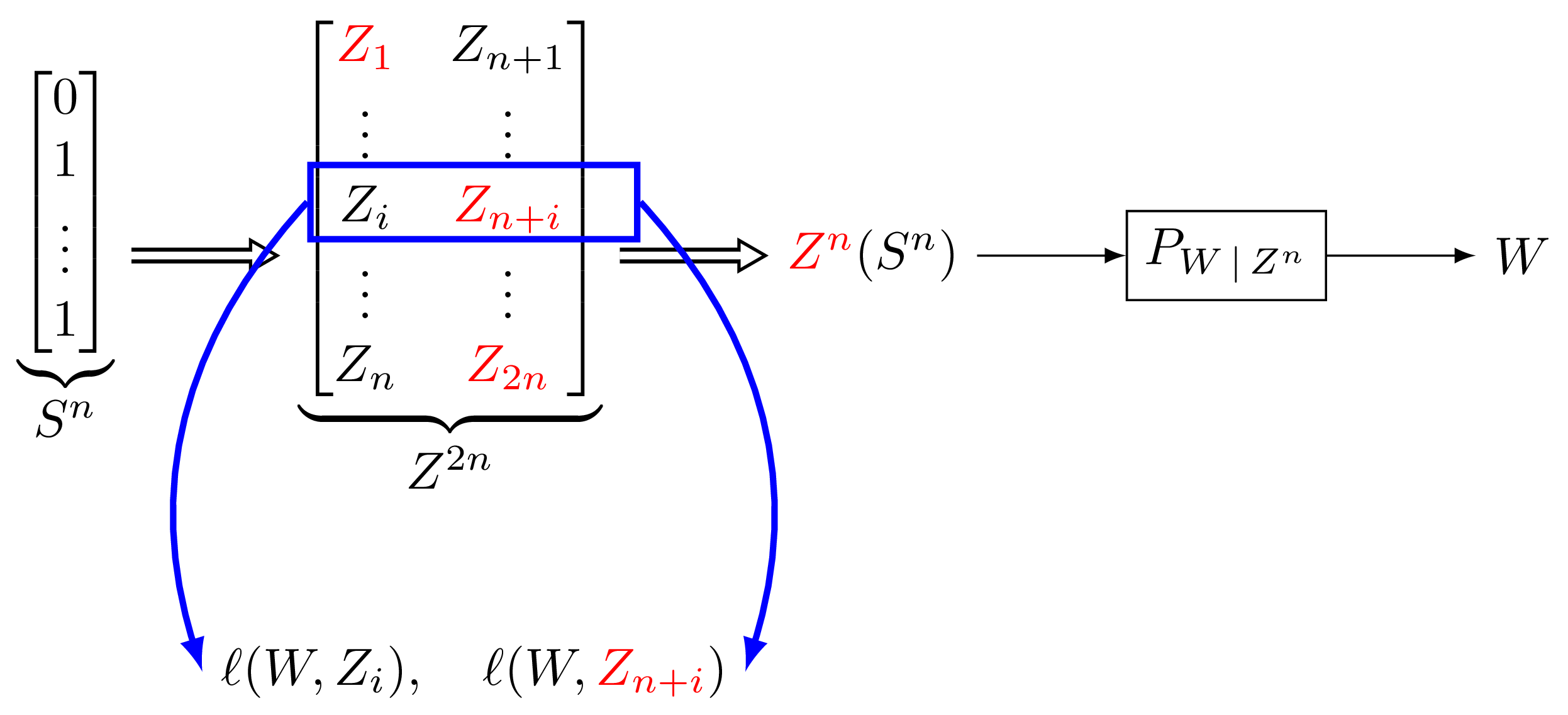
Information-theoretic generalization bounds, i.e., bounds on the generalization error of DNNs that depend on information-theoretic metrics, such as mutual information and relative entropy, have recently emerged as a promising tool to shed lights on the DNN-performance mystery. Indeed, differently from generalization bounds that are in terms of classical statistical learning complexity measures such as VC dimension and Rademacher/Gaussian complexities, information-theoretic bounds, when suitably optimized, have been shown to yield accurate performance predictions for some DNNs scenarios of practical interest.

The goals of this project

The goal of this project is to significantly advance the state of the art in this field by deriving novel information-theoretic generalization bounds that depend on the so-called evaluated conditional mutual information (eCMI). Given two data samples, this quantity describes our ability to guess which one of the two has been used to train the DNN, after we observe the value of the loss function computed at these two data samples. We believe that the eCMI is uniquely suited to shed lights on the theoretical performance of DNNs, since it does not suffer from the disadvantages of the information-theoretic metrics used so far in this context. The specific objectives of the project are:

1. To determine the expressiveness of information-theoretic bounds that are explicit in the eCMI.

2. To demonstrate via comprehensive numerical experiments that bounds based on eCMI describe accurately the generalization performance of DNNs.

3. To explore the use of eCMI bounds in the context of metalearning, where the objective is to facilitate learning of a new task by exploiting training data pertaining to related tasks.

Relevant literature

• T. Steinke and L. Zakynthinou, “Reasoning about generalization via conditional mutual information,” in Conf. Learning Theory (COLT), Jul. 2020. [.pdf]

• H. Harutyunyan, M. Raginsky, G. V. Steeg, and A. Galstyan, “Information-theoretic generalization bounds for black-box learning algorithms,” in Conf. Neural Information Processing Systems (NeurIPS), Dec. 2021. [.pdf]

• M. Haghifam, G. K. Dziugaite, S. Moran, and D. M. Roy, “Towards a unified information-theoretic framework for generalization,” in Conf. Neural Information Processing Systems (NeurIPS), Dec. 2021. [.pdf]

• F. Hellström and G. Durisi, “Nonvacuous loss bounds with fast rates for neural networks via conditional information measures,” in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Sidney, Australia, Jul. 2021. [.pdf]

• A. Rezazadeh, S. T. Jose, G. Durisi, and O. Simeone, “Conditional Mutual Information Bound for Meta Generalization Gap,” in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Sidney, Australia, Jul. 2021. [.pdf]