Generalization Bounds via Information Density and Conditional Information Density
The following paper will appear in the third issue of the IEEE Journal on Selected Areas in Information Theory; this issue focuses on statistical estimation and inference:
F. Hellström and G. Durisi, “Generalization bounds via information density and conditional information density,” IEEE J. Sel. Areas Info. Theory, 2020, to appear. Available on arXiv. Important note: the proof of the data-dependent bounds provided in the paper contains an error, which is rectified in the following document
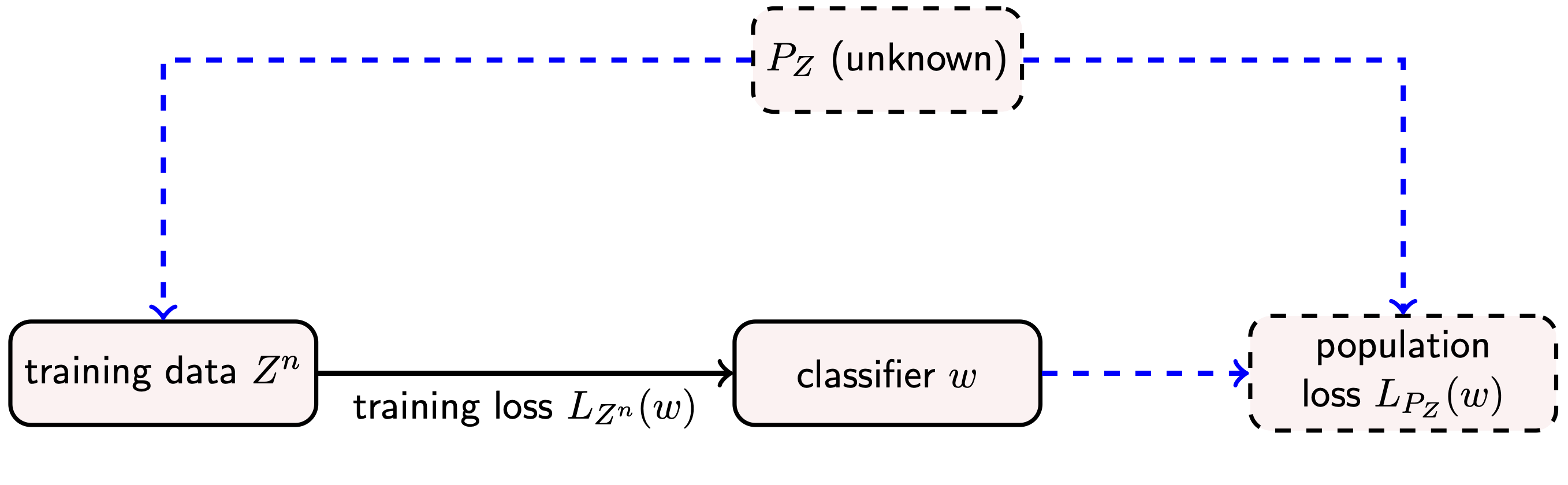
This paper deals with the problem of obtaining information-theoretic bounds on the generalization error of learning algorithms. By information-theoretic, we mean that the bounds are function of information-theoretic metrics capturing the dependence of the output hypothesis on the available training data.
Different notions of generalization error exist in the literature, and the available bounds are obtained using different sets of theoretical tools. In the paper, we present a simple technique that allows one to recover (and sometimes improve on) several of the available bounds. Our approach, which is inspired by results obtained by Catoni, relies on the sub-Gaussianity of the loss function as well as on Markov and Jensen inequalities.
The technique proposed in this paper can also be applied to obtain generalization bounds for the scenario recently introduced by Steinke and Zakynthinou in which only a randomly-selected fraction of the available training data is used. The advantage of this approach, compared to the standard one, is that it can yield tighter generalization bounds, which depend on information-theoretic quantities capturing the conditional dependence of the output hypothesis on the random variable determining the selected training data, given the overall set of available training data.
An open problem in statistical learning theory is to theoretically characterize the performance of modern machine-learning algorithms, such as deep neural networks. As we have recently shown here, the techniques proposed in the paper and the corresponding bounds are promising, since they can be used to obtain nonvacuous estimates of the generalization error of deep neural networks used to classify images from MNIST and fashion-MNIST.


