Massive MIMO for URLLC? Use multicell MMSE processing and avoid pilot contamination
Can massive MIMO be used to support ultra-reliable low-latency (URLLC) applications? And if so, how should it be set up? These are the questions we address in the following paper:
J. Ostman, A. Lancho, G. Durisi, and L. Sanguinetti, “URLLC with Massive MIMO: Analysis and Design at Finite Blocklength,” Sep. 2020. [arXiv]
The design of massive MIMO for systems providing large spectral efficiency is by now well understood. However, most of the design guidelines that have been obtained so far have been developed for the so-called ergodic regime, where each transmitted codeword spans a large number of coherence blocks.
URLLC applications often involve short packets, typically transmitted within the channel coherence time and coherence bandwidth. So each codeword in URLLC applications experiences a quasi-static fading channel, i.e., a constant (but random) channel. This means that we are typically very far away from the ergodic regime.
In the paper, we show that the so called outage framework (outage capacity, outage probability), altough more pertinent to quasi-static channels than the ergodic scenario, cannot be used either to obtain precise design guidelines. Indeed, it yields inaccurate performance predictions when applied to the combination of URLLC plus massive MIMO. And the same conclusion holds for approximations of the maximum coding rate achievable at finite block-length based on the central limit theorem (normal approximations).
It turns out that, to obtain accurate performance predictions, one has to use firm nonasymptotic bound from finite-blocklength information theory. In the paper, we show how to adapt such bounds to massive MIMO systems, and how to evaluate them efficiently and accurately using the so-called saddle-point method.
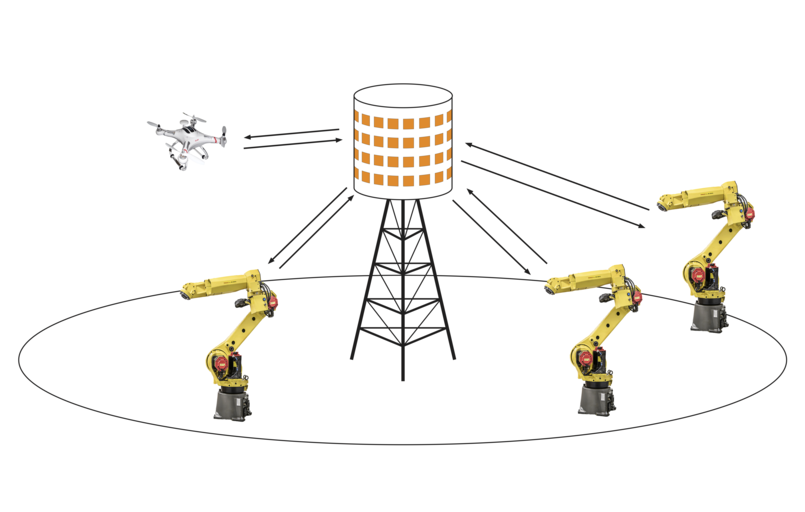
The setup we consider in the paper is fairly general and encompasses imperfect channel state information, pilot contamination, spatially correlated channels, and arbitrary linear spatial processing.
Here is the punchline of our paper: for a practical massive-MIMO setup involving a base station with $100$ antennas, a target error probability of $10^{-5}$ can be achieved over more that $90\%$ of each cell when transmitting short packets only if
-
Multicell-MMSE spatial processing rather than the simpler MR spatial processing is used
-
Pilot contamination is avoided by assigning orthogonal pilot sequences to all users in the system.